huh? That’s awesome! Let’s break down those SSS, SAS, ASA, and AAS congruence postulates together. Don’t worry, I’ll make it as easy as pie, or maybe even easier.
Imagine you’ve got two triangles, and you want to know if they’re exactly the same size and shape. That’s what congruence is all about. Think of it like two identical twins, but instead of people, it’s triangles!
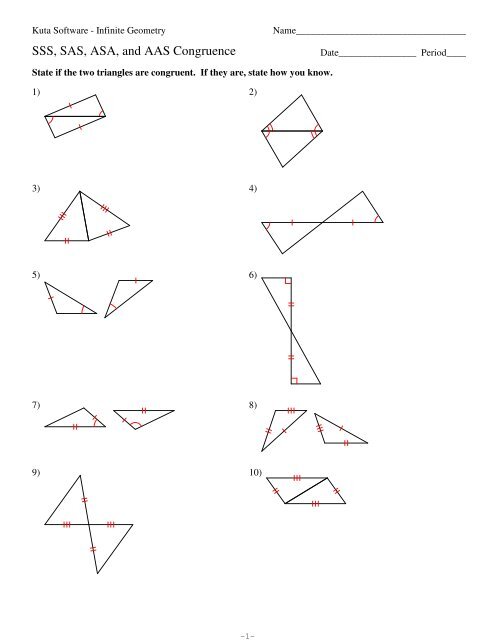
So, how do we know if they’re twins? That’s where our trusty postulates come in. They’re like secret codes, but instead of decoding messages, they tell us how to figure out if two triangles are congruent.
Let’s start with SSS (Side-Side-Side). Think of it like building a triangle with LEGOs. If you know all three sides of one triangle are the same length as the corresponding sides of the other triangle, BAM! You’ve got yourself a pair of congruent triangles. It’s that simple!
Next up is SAS (Side-Angle-Side). Picture this: you know two sides of one triangle are the same length as two corresponding sides of the other triangle, and the angle between those two sides is also the same. Boom! Congruent triangles! It’s like having two matching pieces of a puzzle.
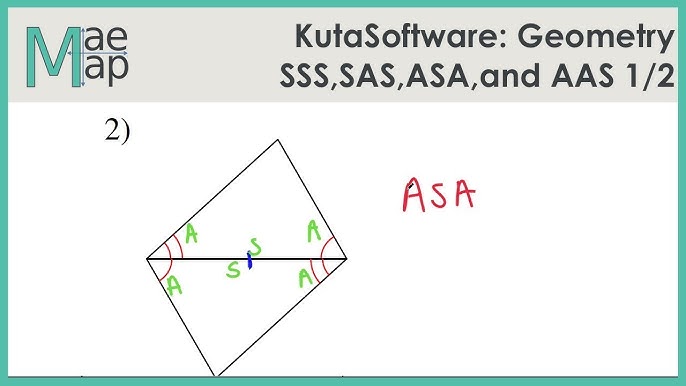
Now, let’s talk about ASA (Angle-Side-Angle). This one’s a bit like a sandwich: you know two angles of one triangle are equal to two corresponding angles of the other triangle, and the side between those angles is also the same. Guess what? You’ve got congruent triangles!
Finally, we’ve got AAS (Angle-Angle-Side). It’s like the SAS postulate’s cousin. You’ve got two angles of one triangle matching two corresponding angles of the other triangle, and a side that’s not between those angles is also the same. Congratulations! Those triangles are twins!
Let’s summarize these postulates in a table, so it’s easier to remember:
| Postulate | Requirements |
|---|---|
| SSS | All three sides of one triangle are equal to the corresponding sides of the other triangle. |
| SAS | Two sides and the included angle of one triangle are equal to the corresponding sides and included angle of the other triangle. |
| ASA | Two angles and the included side of one triangle are equal to the corresponding angles and included side of the other triangle. |
| AAS | Two angles and a non-included side of one triangle are equal to the corresponding angles and non-included side of the other triangle. |
Remember, these postulates are super helpful for proving triangles congruent. So next time you’re working with triangles, try to see if you can use SSS, SAS, ASA, or AAS to determine if they’re congruent. It’s like a puzzle-solving adventure!
So, what are you waiting for? Let’s get those triangles congruent!
What do you think is the most useful congruence postulate? Which one do you find the easiest to remember? Share your thoughts!